金融时间序列分析：Python基于garch模型预测上证指数波动率、计算var和var穿透率、双尾检验

本篇文章分享金融时间序列分析：Python基于garch模型预测上证指数波动率、计算var和var穿透率、双尾检验，对你有帮助的话记得收藏一下，看Python资料网收获更多编程知识

目录

一、收益率波动效应的分析

1.1  收益率序列平稳性检验

1.2 建立AR(p)模型

1.3 Ljung-Box混成检验残差序列的相关性，判断是否有ARCH效应

1.4 建立ARCH模型

 二、GARCH模型与波动率预测

2.1 建立GARCH模型

2.2 波动率预测

三、正态分布的假设下通过波动率计算VaR

 四、厚尾分布的假设下通过波动率计算VaR

五、同在一坐标系中画出股票的损失率图形及VaR图形

六、正态分布及厚尾分布下的VaR穿透率

 本文的研究内容包括以下几个方面：

1.选择上证指数，利用GARCH模型对波动率进行预测；

2.在假设收益率满足正态分布的条件下，利用预测的波动率动态计算VaR；

3.选取适合的重尾分布（如t分布或Gumbel分布），假设收益率满足该分布，利用预测的波动率动态计算VaR；

4.在以上分析的基础上，进行相关图表的绘制；

5.统计正态分布和重尾分布条件下的VaR穿透率，并进行双尾检验。

本文围绕上述问题包含了一整套研究的流程，包括对数据的平稳性检验、残差检验、相关性分析、模型的定阶等。

文字通俗易懂，全面地指导了研究的进行，特别适合新手快速上手。

一、收益率波动效应的分析

通过进行收益率波动效应的分析，我们可以了解到收益率的波动是如何影响市场的，以及波动的原因和机制。

这有助于我们更好地理解金融市场的特点和规律，并为GARCH模型预测提供基础。

1.1  收益率序列平稳性检验

Python绘制收益率随日期变动趋势，如图所示：

根据图片可知，上证指数的收益率曲线呈现出明显的上下波动，波动的振幅较大，在相对短时间内频繁地在某一水平上下波动，形成一种震荡的走势，表明市场或者数据存在较大的不确定性。

通过进一步检验收益率序列的平稳性，决定是否需要进行差分。原假设H0：序列为非平稳的，备择假设H1:序列是平稳的。利用ADF检验可以判断任意时间序列的平稳性，一般情况下，非平稳时间序列存在单位根，可通过差分的方式消除单位根得到平稳序列。

计算得到p-value的值为0.0，小于显著性水平，故拒绝原假设，该收益率序列为平稳的非白噪声序列。

（关注gz号“finance褪黑素”回复222可获取本文全部数据和代码）

1.2 建立AR(p)模型

建立AR均值方程在时间序列分析中是非常常见和重要的步骤。AR均值方程可以用来描述序列的长期趋势和平均水平，可以揭示序列的长期趋势、对序列进行预测和模拟、准确地分离序列中的信号和噪声。通过分析模型系数，我们可以了能够揭示序列长期趋势、进行预测和模拟、分析信号和噪声、以及进行模型检验和优化等重要工具。这些都对我们更好地理解和解释时间序列数据非常有帮助。

根据该收益率序列的自相关函数进一步判定AR(p)模型的阶次，结果如图所示：

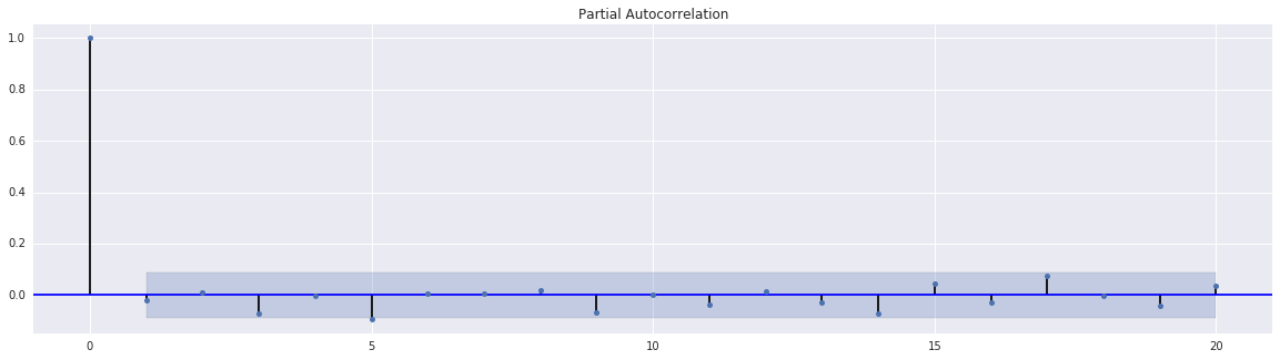
位于阴影内的第一个数为1，因此建立任意1阶及它之后的阶数都可以。作者尝试了几个阶数，发现7的效果最好（波动率的预测效果），因此建立AR(7)的模型。

1.3 Ljung-Box混成检验残差序列的相关性，判断是否有ARCH效应

数据序列具有ARCH效应是建立GARCH模型的前提条件之一。ARCH效应指的是序列中存在自相关的异方差性，即序列的波动程度与之前的波动程度相关。如果一个序列显示出ARCH效应，那么使用ARCH模型无法完全捕捉到其波动特征。

残差及残差平方的时间序列趋势如图所示：

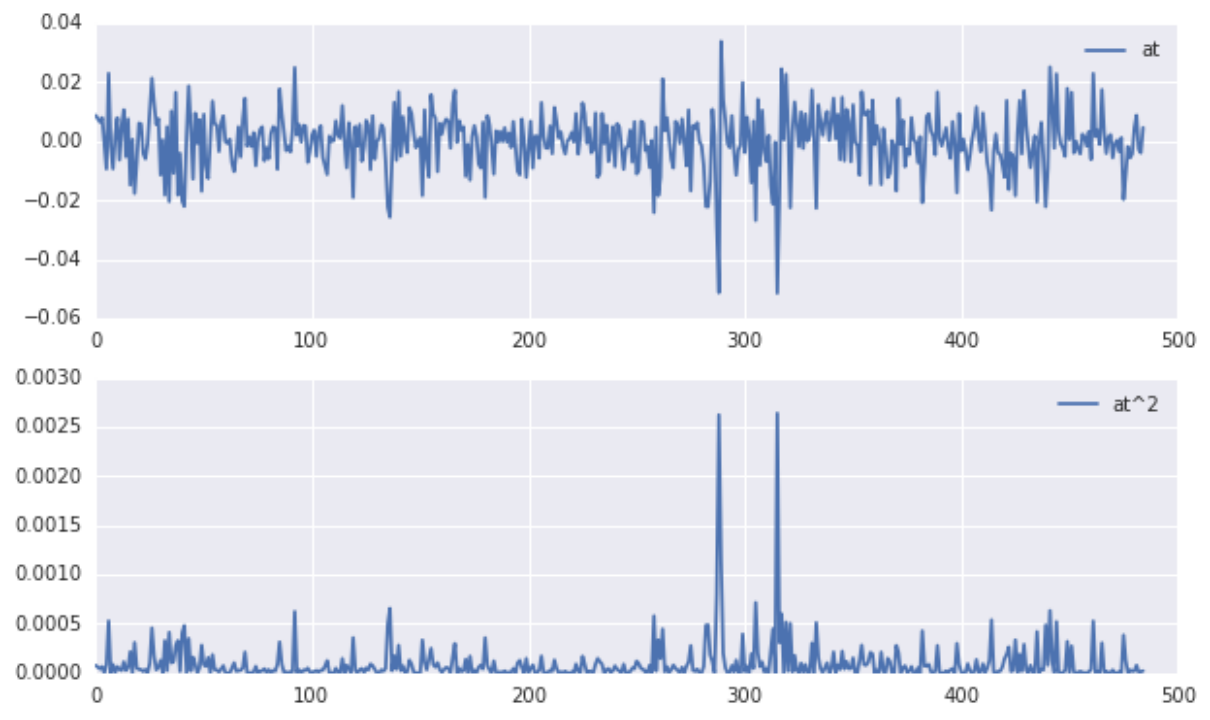
对序列进行混成检验。原假设H0:序列没有相关性，备择假设H1:序列具有相关性。我们检验25个自相关系数：

通过观察上图，我们可以发现在所绘制的序列中，p-value的值均小于显著性水平0.05。由此推断，我们可以拒绝原假设，并且得出结论认为该序列具有相关性。进一步分析显示，残差平方的序列具有ARCH效应。这意味着序列中的波动性具有时间上的相关性和异方差性，即在不同的时间点上波动程度的大小存在明显差异。通过这一观察结果，我们可以深入研究波动模型，以更好地理解和解释序列的波动特性。

1.4 建立ARCH模型

通过对序列进行偏自相关函数（PACF）的分析，我们可以确定最适合的阶次。从下方图中可以观察到，PACF在3阶之后显著下降，因此我们可以将阶次定为3。

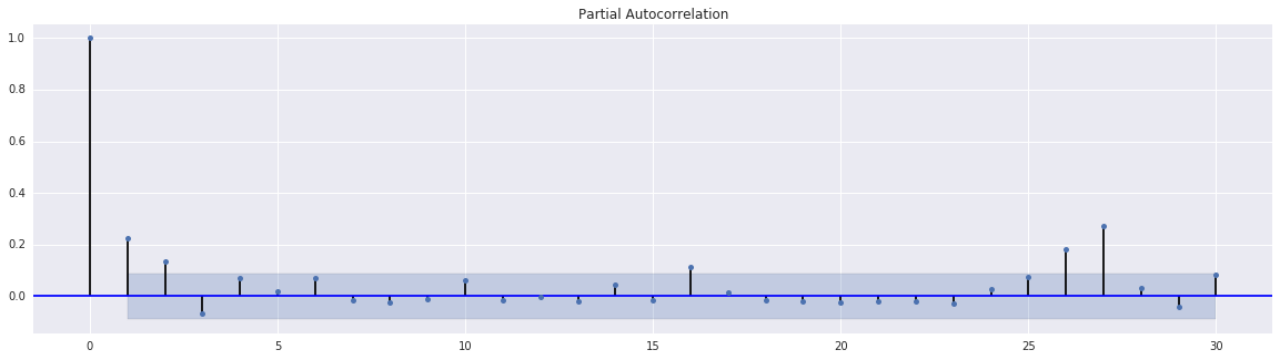
基于此结果，我们可以建立一个ARCH(3)模型，以更好地分析和描述序列的波动特征。ARCH(3)模型是一种常用的时间序列模型，它能够捕捉序列中的波动性和波动特征，从而提供更准确的预测和分析结果。通过使用这个模型，我们可以进一步研究和解释序列中的波动行为，并为后续的分析提供有力的基础。

模型结果如下：

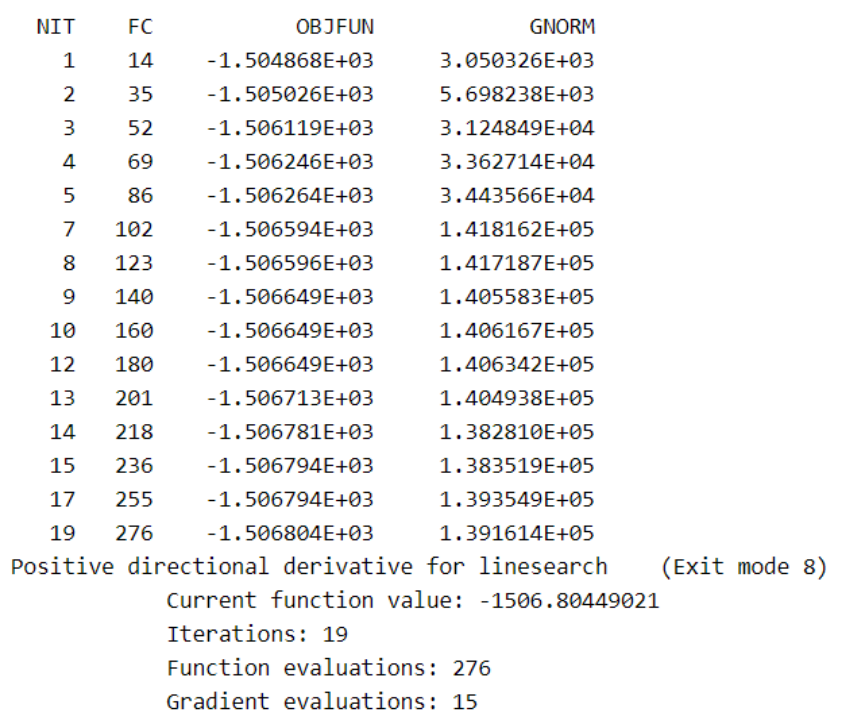
 根据回归结果得到以下方程：

 对上述模型，我们可以看出，沪深300指数的日收益率期望大约在0.073%。并且回归模型的R-squared较小，拟合效果一般。根据拟合的方程进行预测并查看整体的预测拟合情况，从图中可以看出，虽然预测值和实际值的具体数值差距挺大，但是整体上均值和方差的变化相类似。

​​​​​​​（关注gz号“finance褪黑素”回复222可获取本文全部数据和代码）

 二、GARCH模型与波动率预测

2.1 建立GARCH模型

GARCH(m,s)模型的定阶较难，但是据学者们的实证研究结果，我们一般使用低阶模型GARCH(1,1),GARCH(2,1),GARCH(1,2)等就能够基本消除模型的波动性。下面我们构建均值方程为AR(7)模型，波动率模型为GARCH(1,1)的GARCH模型，回归结果如下：

 最终我们得到波动率模型为：

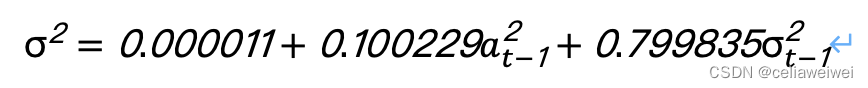
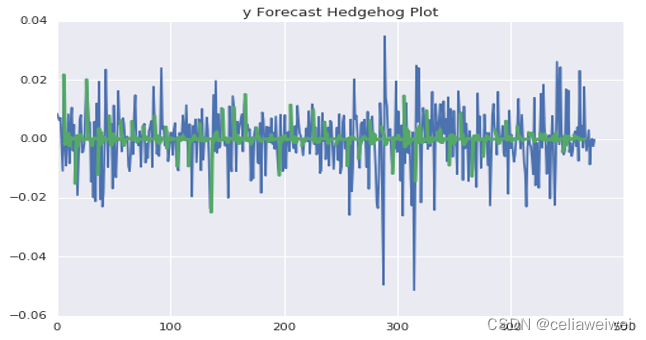
上面第一张图为标准化残差，近似平稳序列，说明模型在一定程度上是正确的；第二张图中绿色为原始收益率序列、蓝色为条件异方差序列，可以发现条件异方差很好得表现出了波动率。 

 上图为方差的拟合图，观察拟合图发现，模型在方差的还原上表现不错。

2.2 波动率预测

接着根据上面得到的波动率模型预测波动率，我们将原始数据、条件异方差拟合数据及预测数据一起画出来，进一步分析波动率预测情况。

 图中红色部分为预测结果，可以看到最终的预测效果较好，基本符合原始数据的波动情况。

三、正态分布的假设下通过波动率计算VaR

利用序列的均值和标准差来描述其分布特征，通过选择置信水平来确定预测VaR的可靠性水平，常见的置信水平为95%或99%，再利用正态分布的累积分布函数逆函数（即Z-score）来计算对应于置信水平的VaR值。VaR代表在未来一定时间内，在给定置信水平下可能达到的最大损失。因此，通过将Z-score与波动率相乘，可以得到预测的波动率VaR。

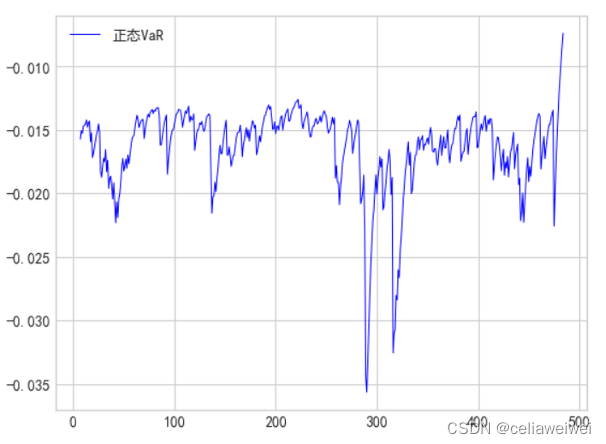
 四、厚尾分布的假设下通过波动率计算VaR

假设股票收益率序列服从t分布的前提下，计算波动率VaR的方法如下：首先，假设股票收益率服从t分布，这种分布能够更好地考虑股票收益率的非正态特征，尤其是在尾部的厚尾现象。然后，通过选择置信水平来确定预测VaR的可靠性水平，常见的置信水平为95%或99%。接下来，利用自由度来描述t分布的形状，自由度通过收益率序列的长度减去1来计算。基于置信水平和自由度，使用t分布的累积分布函数逆函数（t-score）来计算对应于置信水平的VaR值。VaR代表在未来一定时间内，在给定置信水平下可能达到的最大损失。因此，通过将t-score与波动率相乘，可以得到预测的波动率VaR。

五、同在一坐标系中画出股票的损失率图形及VaR图形

六、正态分布及厚尾分布下的VaR穿透率

在金融风险管理领域，VaR（Value at Risk）是一种常用的风险度量指标，用于评估投资组合或资产在一定置信水平下的最大可能损失。在计算VaR时，常常需要假设股票收益率的概率分布模型。

在假设股票收益率服从正态分布的情况下，可以通过计算收益率序列的均值和标准差，确定在给定置信水平下的VaR值。VaR穿透率表示实际损失超过VaR值的概率。在正态分布假设下，较低的VaR穿透率表示较好的风险控制能力。然而，在实际情况中，股票收益率往往呈现出厚尾分布的特征，即存在较多的极端事件和离群值。为了更准确地估计风险，可以使用厚尾分布来近似股票收益率的分布特征。常用的方法是使用t分布来近似厚尾分布，通过选择合适的自由度参数来计算VaR值。由于考虑了较多的极端情况，厚尾分布下的VaR穿透率通常较高。

此外，为进一步检查收益率序列中是否存在显著的极端值，本文分别对其进行双尾检验。在正态分布假设下。可以使用标准正态分布表或正态分布的临界值进行双尾检验。而在厚尾分布假设下，需要使用t分布的临界值进行双尾检验。通过计算双尾检验通过率，可以评估超过临界值的极端事件的概率。较低的双尾检验通过率表示较小的极端事件风险。

沪深300指数的结果如下：

正态分布下的VaR穿透率： 0.05155

厚尾分布下的VaR穿透率： 0.20672

正态分布下的双尾检验通过率： 0.0

厚尾分布下的双尾检验通过率： 0.0

​​​​​​​​​​​​​​（关注gz号“finance褪黑素”回复222可获取本文全部数据和代码）

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！