Python多元非线性回归及绘图

文章Python多元非线性回归及绘图分享给大家，欢迎收藏Python资料网，专注分享技术知识

Python多元非线性回归及绘图

在数字地形模型这门课做的一个小实验，代码实现的是以影像因子和地形要素为自变量，采样后的高程计算出的指标为因变量进行回归，本质上是通过curve_fit进行多元非线性回归，但是当时的要素偏多，需要写代码依次使用不同的自变量和因变量回归

环境：Python 3.9

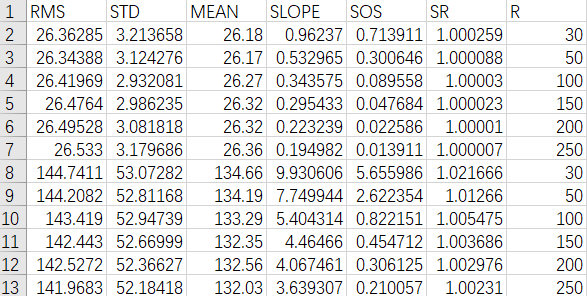
部分数据截图

代码逻辑

导入所需库和模块

# coding=gbk
# -*- coding = utf-8 -*-

import numpy as np
import pandas as pd
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

• numpy：用于数值计算和数组操作。
• pandas：用于读取和处理Excel数据。
• scipy.optimize.curve_fit：用于非线性最小二乘拟合。
• matplotlib.pyplot：用于绘制三维散点图和曲面。

定义非线性模型函数

def nonlinear_model(xy, a, b, c):
    x, y = xy
    return (a * x - b) * y + c

定义nonlinear_model函数，它接受两个坐标xy（包含x和y的元组）以及三个参数a, b, c，即 (a * x - b) * y + c

设置数据源和变量

excel_file_path = 'E:\zbh.xlsx'    
df = pd.read_excel(excel_file_path)

x = 'R'
y = 'SOS'
z = 'MEAN'
x_data = np.array(df[x])
y_data = np.array(df[y])
z_data = np.array(df[z])

指定的Excel文件路径可以改改，读取变量R, SOS, MEAN的列数据，这里也需要根据数据本身来改

非线性回归与参数估计

popt, pcov = curve_fit(nonlinear_model, (x_data, y_data), z_data)
a_fit, b_fit, c_fit = popt
z_fit = nonlinear_model((x_data, y_data), a_fit, b_fit, c_fit)

使用scipy.optimize.curve_fit对给定的nonlinear_model函数进行拟合，传入观测到的(x_data, y_data)对和对应的z_data作为目标值。curve_fit返回最佳拟合参数popt和协方差矩阵pcov。接着，将最佳参数赋值给a_fit, b_fit, c_fit，并使用这些参数计算出所有数据点的拟合值z_fit。

计算拟合优度指标和均方根误差

ss_total = np.sum((z_data - np.mean(z_data)) ** 2)
ss_reg = np.sum((z_fit - np.mean(z_data)) ** 2)
r_squared = ss_reg / ss_total
rmse = np.sqrt(np.mean((z_data - z_fit) ** 2))

print("R方:", r_squared)
print("RMSE:", rmse)

计算拟合优度指标（R方），均方根误差（RMSE），最后打印

构建拟合公式字符串

formula = "{} = ({:.2f} * {} + ({:.2f})) * {} + {:.2f}".format(z, a_fit, x, b_fit, y, c_fit)
print(formula)

用已得到的最佳参数和变量名构建最终的拟合公式，并保留两位小数精度。

绘制三维散点图和拟合曲面

fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection='3d')

ax.scatter(x_data, y_data, z_data, color='blue', label='Data Points')
X, Y = np.meshgrid(np.linspace(min(x_data), max(x_data), 30),
                   np.linspace(min(y_data), max(y_data), 30))
Z = nonlinear_model((X.flatten(), Y.flatten()), a_fit, b_fit, c_fit).reshape(X.shape)
ax.plot_surface(X, Y, Z, color='r', alpha=0.6, label='Fitted Surface')

ax.set_xlabel(x)
ax.set_ylabel(y)
ax.set_zlabel(z)
plt.title(x +"-"+ y + "-" + z + ":" + formula)
plt.show()

计算Z值和绘图

完整代码

# coding=gbk
# -*- coding = utf-8 -*-

import numpy as np
import pandas as pd
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# 定义非线性模型函数
def nonlinear_model(xy, a, b, c):
    x, y = xy
    return (a * x - b) * y + c

# 指定Excel文件路径并读取
excel_file_path = 'E:\zbh.xlsx'
df = pd.read_excel(excel_file_path)
x = 'R'
y = 'SOS'
z = 'MEAN'
x_data = np.array(df[x])
y_data = np.array(df[y])
z_data = np.array(df[z])

# 利用 curve_fit 进行非线性回归
popt, pcov = curve_fit(nonlinear_model, (x_data, y_data), z_data)
a_fit, b_fit, c_fit = popt
z_fit = nonlinear_model((x_data, y_data), a_fit, b_fit, c_fit)

# 计算指标
ss_total = np.sum((z_data - np.mean(z_data)) ** 2)
ss_reg = np.sum((z_fit - np.mean(z_data)) ** 2)
r_squared = ss_reg / ss_total
rmse = np.sqrt(np.mean((z_data - z_fit) ** 2))
print("R方:", r_squared)
print("RMSE:", rmse)
# 拟合公式
formula = "{} = ({:.2f} * {} + ({:.2f})) * {} + {:.2f}".format(z, a_fit, x, b_fit, y, c_fit)
print(formula)

# 绘制三维散点图和拟合曲面
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection='3d')

# 散点图
ax.scatter(x_data, y_data, z_data, color='blue', label='Data Points')
# 曲面图
X, Y = np.meshgrid(np.linspace(min(x_data), max(x_data), 30),
                   np.linspace(min(y_data), max(y_data), 30))
Z = nonlinear_model((X.flatten(), Y.flatten()), a_fit, b_fit, c_fit).reshape(X.shape)
ax.plot_surface(X, Y, Z, color='r', alpha=0.6, label='Fitted Surface')

ax.set_xlabel(x)
ax.set_ylabel(y)
ax.set_zlabel(z)
plt.title(x +"-"+ y + "-" + z + ":" + formula)
plt.show()

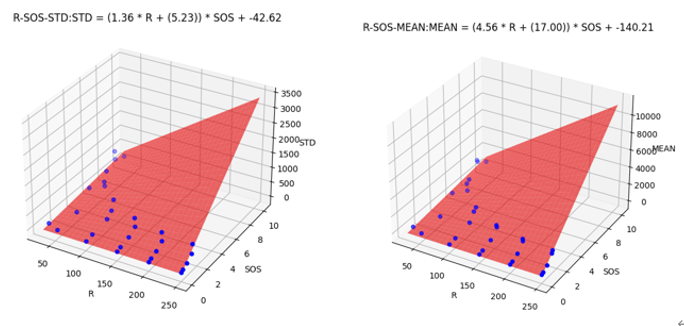
部分结果

总结

由于这次实验用到的数据量较少，因此画图的效果感觉一般，趋势不明显，计算出的指标参考意义也有限，数据量大一点效果好坏会一目了然

参考

Matplotlib文档
Scipy Curve_fit文档

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！