Python 数据结构——二叉树（最最最最最实用的二叉树教程）

本篇文章分享Python 数据结构——二叉树（最最最最最实用的二叉树教程），对你有帮助的话记得收藏一下，看Python资料网收获更多编程知识

本文章以实用为主，所以不多废话直接开整

本文所介绍的二叉树是最基础的二叉树，不是二叉搜索树，也不是平衡二叉树，就基本的二叉树

二叉树的创建

基本二叉树的创建其实比链表还要简单，只需创建一个节点的类即可，随后用指针将其串起来。不同于链表的是，二叉树为一个父节点连接到两个子节点，若还要加入新的节点，那么此时的子节点将会变成新加入节点的父节点，以此类推，每一个父节点最多只有两个节点（所以叫二叉树）
 

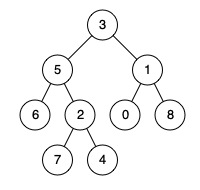
我们将上述图中的二叉树写成代码的形式（如下） 

class node:
    def __init__(self,data):
        self.data = data
        self.right = None
        self.left = None

tree = node(3)
tree.left = node(5)
tree.right = node(1)
tree.left.left = node(6)
tree.left.right = node(2)
tree.right.left = node(0)
tree.right.right = node(8)
tree.left.right.left = node(7)
tree.left.right.right = node(4)

创建基础二叉树代码

tree = node(data)  #  表示最初的祖先节点

tree.left = node(data)  #  表示祖先节点的左孩子

tree.right = node(data)  #  表示祖先节点的右孩子

tree.left.left = node(data)  #  表示祖先节点的左孩子的左孩子

..............................

以此类推即可，有点类似于套娃

二叉树的遍历

二叉树的遍历有别于线性表的遍历，很明显，二叉树是一个复杂的二维结构，所以二叉树有很多不同的遍历方法，其中常见的是：先序遍历，中序遍历，后序遍历以及层序遍历

先序遍历

先序遍历，中序遍历，后序遍历其实本质上都差不多，只不过是遍历顺序的不同罢了

先序遍历：就是先遍历根节点，其次是左孩子，最后是右孩子

def preorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.append(root.data)
        result.extend(preorder_traversal(root.left))
        result.extend(preorder_traversal(root.right))
        return result

上述代码中，我们通过递归的方式遍历二叉树，可能有点小难懂，我来仔细解释一下：

此函数其实每次都会往 result 内塞入一个节点，即当前节点，随后对左子树进行递归，然后对子树进行递归，即可完成  根->左->右  的遍历，即先序遍历

知道上述代码的逻辑之后，稍微修改一些即可得到中序遍历以及后序遍历

中序遍历

中序遍历：就是先遍历左孩子，其次是根节点，最后是右孩子

def inorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.extend(inorder_traversal(root.left))
        result.append(root.data)
        result.extend(inorder_traversal(root.right))
        return result

有没有发现上述代码和有点小眼熟，其实上述代码就是先序遍历的代码只不过调换了 result 元素纳入的顺序罢了，即交换了两行代码而已，就可得到中序遍历的代码

后序遍历

后序遍历：就是先遍历左孩子，其次是右孩子，最后是根节点

def postorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.extend(postorder_traversal(root.left))
        result.extend(postorder_traversal(root.right))
        result.append(root.data)
        return result

此时或许你已经可以举一反三了，也不用我过多的解释了，将根节点的插入放到最后即可得到后序遍历的代码

层次遍历

在这里你就要稍微注意一下了，层序遍历有别于先序中序后序遍历，层序遍历是按树的高度进行遍历的，即现遍历最上面的一层，随后是第二层，再就是第三层.......等等等等

def level_order_traversal(root):
    if root is None:
        return
    else:
        result = []
        queue = [root]
        while queue:
            current_level = []
            for i in range(len(queue)):
                node = queue.pop(0)
                current_level.append(node.data)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            result.append(current_level)
        return result

我们可以借助队列，队列的性质是先进先出（FIFO），首先将根节点加入到队列中，随后开始遍历，不过要注意的是，此时的队列是动态的：

当node存在左节点或者右节点的时候队列queue将会把node的左右孩子存入其中（哪个孩子存在，就将哪个孩子存入其中），随后继续进行遍历

上述代码中最后返回为一个二维数组，当然如果你需要也可以将其改为一维数组，删除current_level即可

常见的二叉树操作

在LeetCode上刷题你就会发现，那些基础题的解决方法大差不差，其本质是以下三种方法的变式而已，只要熟练下列常规操作，你就可以秒杀绝大多数基础题

返回树的深度

聪明的你已经返现了，当你熟练掌握二叉树的层序遍历后，只要你能得到层序遍历的层数，你就能得到二叉树的深度

def root_depth(root):
    return len(level_order_traversal(root))

没错，就是这么简单 

返回树的节点个数

聪明的你又发现了，当你熟练掌握二叉树的  先序遍历/中序遍历/后序遍历  之后，你就会发现，其实只要你知道遍历后返回的数组或者列表内的元素个数即可

def node_nums(root):
    return len(inorder_traversal(root))

没错，就是这么的简单 

寻找某个节点的父节点

其实不会有问题问你让你在某二叉树中寻找一个已知的节点，她会变着法的靠你对二叉树遍历的熟练度，比如找某两个节点公共祖先等等等等，所以与其掌握如何知道一个已知节点的位置，不如掌握如何知道一个未知节点的值

聪明的你又发现了，这道题可能有点小难，不过你思考之后发现其本质和二叉树的遍历类似，只要让其在特等条件下返回某个值即可

def find_ancestor(root, num):
    if root is None:
        return None
    if root.data == num or (root.left and root.left.data == num) or (root.right and root.right.data == num):
        return root.data
    left = find_ancestor(root.left, num)
    right = find_ancestor(root.right, num)
    if left:
        return left
    return right

完整代码

class node:
    def __init__(self,data):
        self.data = data
        self.right = None
        self.left = None

def preorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.append(root.data)
        result.extend(preorder_traversal(root.left))
        result.extend(preorder_traversal(root.right))
        return result


def inorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.extend(inorder_traversal(root.left))
        result.append(root.data)
        result.extend(inorder_traversal(root.right))
        return result

def postorder_traversal(root):
    if root is None:
        return []
    else:
        result = []
        result.extend(postorder_traversal(root.left))
        result.extend(postorder_traversal(root.right))
        result.append(root.data)
        return result

def level_order_traversal(root):
    if root is None:
        return
    else:
        result = []
        queue = [root]
        while queue:
            current_level = []
            for i in range(len(queue)):
                node = queue.pop(0)
                current_level.append(node.data)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            result.append(current_level)
        return result


def root_depth(root):
    return len(level_order_traversal(root))

def node_nums(root):
    return len(inorder_traversal(root))


def find_ancestor(root, num):
    if root is None:
        return None
    if root.data == num or (root.left and root.left.data == num) or (root.right and root.right.data == num):
        return root.data
    left = find_ancestor(root.left, num)
    right = find_ancestor(root.right, num)
    if left:
        return left
    return right



tree = node(3)
tree.left = node(5)
tree.right = node(1)
tree.left.left = node(6)
tree.left.right = node(2)
tree.right.left = node(0)
tree.right.right = node(8)
tree.left.right.left = node(7)
tree.left.right.right = node(4)


print(preorder_traversal(tree))
print(inorder_traversal(tree))
print(postorder_traversal(tree))
print(level_order_traversal(tree))
print(root_depth(tree))
print(find_ancestor(tree, 4))
print(node_nums(tree))

希望本文章对你有所帮助，也请你点点关注支持一下博主，若有什么问题可在评论区评论，博主会第一时间赶到现场，下期博主会带来二叉搜索树与平衡二叉树等更高级二叉树的运用，当然也不要忘了最最重要的，那就是：

自己试试看吧，你会做得更好！

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！