碰撞检测 | 图解视线生成Bresenham算法(附ROS C++/Python/Matlab实现)

Python资料网推荐碰撞检测 | 图解视线生成Bresenham算法(附ROS C++/Python/Matlab实现)这篇文章给大家，欢迎收藏Python资料网享受知识的乐趣

0 专栏介绍

🔥课设、毕设、创新竞赛必备！🔥本专栏涉及更高阶的运动规划算法轨迹优化实战，包括：曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等)，每个算法都包含代码实现加深理解

🚀详情：运动规划实战进阶：轨迹优化篇

---

1 Bresenham算法介绍

Bresenham视线生成算法是一种高效的算法，用于在二维网格上绘制直线。它是由Jack Bresenham在1962年提出的，广泛应用于计算机图形学和游戏开发中。该算法的主要优点是只使用整数运算，因此速度较快且易于实现。下面是该算法的动图案例

Bresenham算法可以巧妙地应用在栅格地图中进行一维碰撞检测：首先确定起点和终点，然后使用Bresenham算法绘制从起点到终点的线段，接着检查该路径上每个栅格点是否与障碍物重叠。

2 图解Bresenham算法

Bresenham碰撞测试在三种类型的移动中访问单元格：

• $x$方向移动
• $y$方向移动
• 对角线移动

在栅格地图中，碰撞检测点连线经过若干离散栅格，因此每次移动都将产生非连续误差，Bresenham算法要求下一个移动偏差最小。通过迭代即可访问检测线经过的所有栅格，判断这些栅格的代价是否超过阈值即可完成碰撞检测。

具体地，设需要检测节点$v$、$w$间的连线是否经过障碍物，定义缩放误差分别为 δ x = ∣ w . x − v . x ∣ \delta _x=\left| w.x-v.x \right| δx​=∣w.x−v.x∣、 δ y = ∣ w . y − v . y ∣ \delta _y=\left| w.y-v.y \right| δy​=∣w.y−v.y∣；扩展误差分别为 e x e_x ex​、 e y e_y ey​；方向增量分别为$\Delta x=sgn\left(w.x-v.x\right)$、$\Delta y=sgn\left(w.y-v.y\right)$。下面考虑 δ x > δ y \delta _x>\delta _y δx​>δy​的情形， δ x ⩽ δ y \delta _x\leqslant \delta _y δx​⩽δy​时可对称导出。

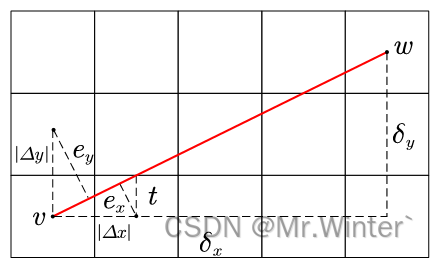
如图所示，根据三角形相似关系可得

{ e y e x = ∣ Δ y ∣ t t δ y = ∣ Δ x ∣ δ x ⇒ e y e x = ∣ Δ y ∣ ∣ Δ x ∣ ⋅ δ x δ y = δ x δ y \begin{cases} \frac{e_y}{e_x}=\frac{\left| \varDelta y \right|}{t}\\ \frac{t}{\delta _y}=\frac{\left| \varDelta x \right|}{\delta _x}\\\end{cases}\Rightarrow \frac{e_y}{e_x}=\frac{\left| \varDelta y \right|}{\left| \varDelta x \right|}\cdot \frac{\delta _x}{\delta _y}=\frac{\delta _x}{\delta _y} {ex​ey​​=t∣Δy∣​δy​t​=δx​∣Δx∣​​⇒ex​ey​​=∣Δx∣∣Δy∣​⋅δy​δx​​=δy​δx​​

不妨令 e y = δ x e_y=\delta _x ey​=δx​、 e x = δ y e_x=\delta _y ex​=δy​，则沿$x$方向移动将产生负向偏差 δ y \delta _y δy​，沿$y$方向移动将产生正向偏差 δ x \delta _x δx​，根据最小化偏差原则选择移动方向

( x , y ) ← { ( x + Δ x , y ) , i f ∣ e + δ x ∣ > ∣ e − δ y ∣ ( x , y + Δ y ) , i f ∣ e + δ x ∣ < ∣ e − δ y ∣ ( x + Δ x , y + Δ y ) , i f ∣ e + δ x ∣ = ∣ e − δ y ∣ \left( x,y \right) \gets \begin{cases} \left( x+\varDelta x,y \right) , \mathrm{if} \left| e+\delta _x \right|>\left| e-\delta _y \right|\\ \left( x,y+\varDelta y \right) , \mathrm{if} \left| e+\delta _x \right|<\left| e-\delta _y \right|\\ \left( x+\varDelta x,y+\varDelta y \right) , \mathrm{if} \left| e+\delta _x \right|=\left| e-\delta _y \right|\\\end{cases} (x,y)←⎩⎪⎨⎪⎧​(x+Δx,y),if∣e+δx​∣>∣e−δy​∣(x,y+Δy),if∣e+δx​∣<∣e−δy​∣(x+Δx,y+Δy),if∣e+δx​∣=∣e−δy​∣​

下图为Bresenham扩展节点的实例

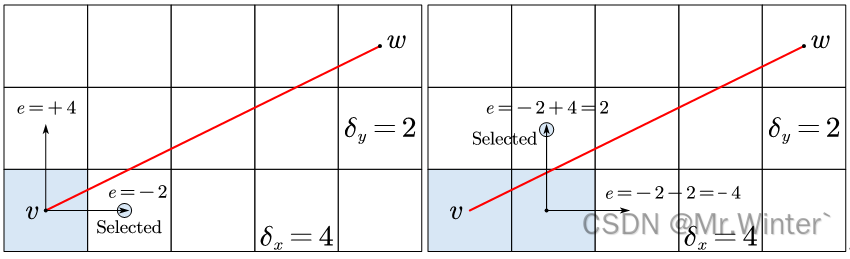
3 算法流程

算法流程如下所示

4 仿真实现

4.1 ROS C++实现

核心代码如下所示

template <typename Point, typename F_is_obs>
static bool BresenhamCollisionDetection(const Point& pt1, const Point& pt2, F_is_obs func_is_obs)
{
  int s_x = (pt1.x() - pt2.x() == 0) ? 0 : (pt1.x() - pt2.x()) / std::abs(pt1.x() - pt2.x());
  int s_y = (pt1.y() - pt2.y() == 0) ? 0 : (pt1.y() - pt2.y()) / std::abs(pt1.y() - pt2.y());
  int d_x = std::abs(pt1.x() - pt2.x());
  int d_y = std::abs(pt1.y() - pt2.y());

  // check if any obstacle exists between pt1 and pt2
  if (d_x > d_y)
  {
    int tau = d_y - d_x;
    int x = pt2.x(), y = pt2.y();
    int e = 0;
    while (x != pt1.x())
    {
      if (e * 2 > tau)
      {
        x += s_x;
        e -= d_y;
      }
      else if (e * 2 < tau)
      {
        y += s_y;
        e += d_x;
      }
      else
      {
        x += s_x;
        y += s_y;
        e += d_x - d_y;
      }
      if (func_is_obs(Point(x, y)))
        // obstacle detected
        return true;
    }
  }
  else
  {
    // similar. swap x and y
    int tau = d_x - d_y;
    int x = pt2.x(), y = pt2.y();
    int e = 0;
    while (y != pt1.y())
    {
      if (e * 2 > tau)
      {
        y += s_y;
        e -= d_x;
      }
      else if (e * 2 < tau)
      {
        x += s_x;
        e += d_y;
      }
      else
      {
        x += s_x;
        y += s_y;
        e += d_y - d_x;
      }
      if (func_is_obs(Point(x, y)))
        // obstacle detected
        return true;
    }
  }
  return false;
}

4.2 Python实现

核心代码如下所示

def BresenhamCollisionDetection(self, node1: Node, node2: Node) -> bool:
	if node1.current in self.obstacles or node2.current in self.obstacles:
	    return False
	
	x1, y1 = node1.current
	x2, y2 = node2.current
	
	if x1 < 0 or x1 >= self.env.x_range or y1 < 0 or y1 >= self.env.y_range:
	    return False
	if x2 < 0 or x2 >= self.env.x_range or y2 < 0 or y2 >= self.env.y_range:
	    return False
	
	d_x = abs(x2 - x1)
	d_y = abs(y2 - y1)
	s_x = 0 if (x2 - x1) == 0 else (x2 - x1) / d_x
	s_y = 0 if (y2 - y1) == 0 else (y2 - y1) / d_y
	x, y, e = x1, y1, 0
	
	# check if any obstacle exists between node1 and node2
	if d_x > d_y:
	    tau = (d_y - d_x) / 2
	    while not x == x2:
	        if e > tau:
	            x = x + s_x
	            e = e - d_y
	        elif e < tau:
	            y = y + s_y
	            e = e + d_x
	        else:
	            x = x + s_x
	            y = y + s_y
	            e = e + d_x - d_y
	        if (x, y) in self.obstacles:
	            return False
	# swap x and y
	else:
	    tau = (d_x - d_y) / 2
	    while not y == y2:
	        if e > tau:
	            y = y + s_y
	            e = e - d_x
	        elif e < tau:
	            x = x + s_x
	            e = e + d_y
	        else:
	            x = x + s_x
	            y = y + s_y
	            e = e + d_y - d_x
	        if (x, y) in self.obstacles:
	            return False
	
	return True

4.3 Matlab实现

核心代码如下所示

function flag = BresenhamCollisionDetection(map, node1, node2)
% @breif: Judge collision when moving from node1 to node2 using Bresenham.
    if (map(node1(1), node1(2)) == 2) || (map(node2(1), node2(2)) == 2)
        flag = true;
        return
    end
    x1 = node1(1); y1 = node1(2);
    x2 = node2(1); y2 = node2(2);
    
    d_x = abs(x2 - x1);
    d_y = abs(y2 - y1);
    if  (x2 - x1) == 0
        s_x = 0;
    else
        s_x = (x2 - x1) / d_x;
    end
    if  (y2 - y1) == 0
        s_y = 0;
    else
        s_y = (y2 - y1) / d_y;
    end
    x = x1; y = y1; e = 0;
    
    % check if any obstacle exists between node1 and node2
    if d_x > d_y
        tao = (d_y - d_x) / 2;
        while x ~= x2
            if e > tao
                x = x + s_x;
                e = e - d_y;
            elseif e < tao
                y = y + s_y;
                e = e + d_x;
            else
                x = x + s_x;
                y = y + s_y;
                e = e + d_x - d_y;
            end
            if map(x, y) == 2
                flag = true;
                return;
            end
        end
    % swap x and y
    else
        tao = (d_x - d_y) / 2;
        while y ~= y2
            if e > tao
                y = y + s_y;
                e = e - d_x;
            elseif e < tao
                x = x + s_x;
                e = e + d_y;
            else
                x = x + s_x;
                y = y + s_y;
                e = e + d_y - d_x;
            end
            if map(x, y) == 2
                flag = true;
                return;
            end
        end
    end
    flag = false;
end

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！