基于图论的时间序列数据平稳性与连通性分析：利用图形、数学和 Python 揭示时间序列数据中的隐藏模式

这篇文章介绍了基于图论的时间序列数据平稳性与连通性分析：利用图形、数学和 Python 揭示时间序列数据中的隐藏模式，分享给大家做个参考，收藏Python资料网收获更多编程知识

时间序列数据表示了一个随时间记录的值的序列。理解这些序列内部的关系,尤其是在多元或复杂的时间序列数据中,不仅仅局限于随时间绘制数据点(这并不是说这种做法不好)。通过将时间序列数据转换为图,我们可以揭示数据片段内部隐藏的连接、模式和关系,帮助我们发现平稳性和时间连通性等性质，这就是图论发挥作用的地方。

在本文中,我们将探讨图论如何洞察时间关系和平稳性，将介绍基于图的变换的基本概念,讨论时间序列数据的平稳性,并展示如何应用这些概念。

什么是时间序列数据的平稳性?

平稳性是时间序列分析中的一个核心概念。如果一个时间序列的统计特性——均值、方差和自相关性——随时间保持不变,则称该时间序列是平稳的。简而言之,平稳时间序列不随时间变化而出现趋势、周期性或变化的方差。

从数学角度来看,如果满足以下条件,则时间序列**X(t)**是平稳的:

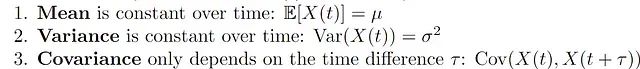
平稳性有助于确保在序列样本中观察到的模式能代表整个数据集。这在预测中至关重要,因为非平稳数据通常会导致不准确或有偏差的模型。

利用图论理解平稳性和连通性

图论作为一个研究网络的数学框架,为表示和分析时间序列数据中的关系提供了强大的工具。图由节点(顶点)组成,节点之间由边连接,边可以表示时间序列数据中状态之间的关系、依赖或转换。

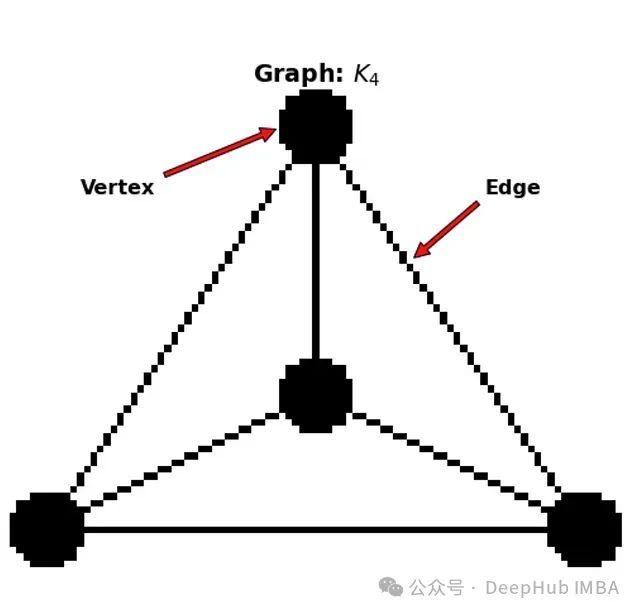
在时间序列分析中,我们可以使用图来模拟时间序列片段内部和之间的依赖关系,揭示周期性和平稳性等关系。

将时间序列转换为图

为了在时间序列分析中应用图论,我们需要将数据转换为图结构。以下是实现这一转换的步骤:

1. 将时间序列划分为片段 :将时间序列划分为相等的部分或我们要分析的区间。
2. 计算成对相似性 :对于每一对片段,计算一个相似性度量,例如互相关或互信息,以定义节点(片段)之间的边。
3. 构建图 :将每个片段视为一个节点,并用它们的相似性加权的边连接节点。

让我们通过一个实例进一步分解这些步骤。

1、分割时间序列

给定一个时间序列X={x1,x2,…,xN},将其划分为 M 个片段,每个片段包含 L 个时间步长(其中 L = N/M)。这会产生片段 X1,X2,…,XM。

2、计算成对相似性

对于每一对片段,计算一个相似性度量 s(i,j)。常见的选择包括:

• 皮尔逊相关系数 :度量片段之间的线性相关性:

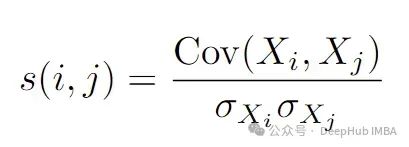
• 动态时间规整(DTW) :通过对齐可能具有非线性时移的片段来捕捉相似性。

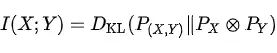
• 互信息 :量化片段之间共享的信息。

较高的相似性值 s(i,j)表示片段之间的连接更强,暗示时间连通性或平稳模式。

3、构建图

创建一个图 G=(V,E),其中:

• V 表示作为节点的片段。
• E 包括节点之间的边,如果它们的相似性超过阈值 α,则边的权重为 w(i,j)=s(i,j)。

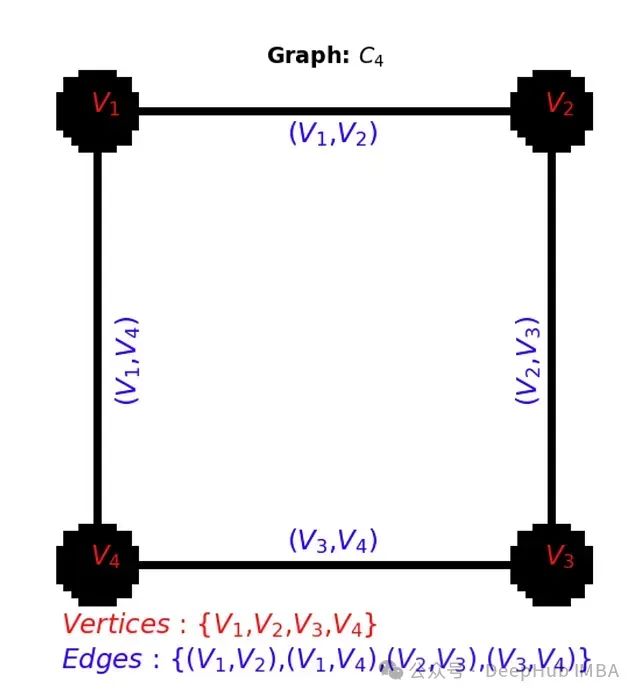
简单示例

以下是使用皮尔逊相关系数创建相似图的简单示例:

 importnumpyasnp
 importnetworkxasnx
 importmatplotlib.pyplotasplt
 fromscipy.statsimportpearsonr
 
 # 模拟时间序列数据
 time_series=np.sin(np.linspace(0, 10*np.pi, 1000)) +np.random.normal(0, 0.1, 1000)
 
 M=20
 L=len(time_series) //M
 segments= [time_series[i*L:(i+1) *L] foriinrange(M)]
 
 # 计算片段之间的相似性(皮尔逊相关系数)  
 G=nx.Graph()
 foriinrange(M):
     G.add_node(i)
     forjinrange(i+1, M):
         corr, _=pearsonr(segments[i], segments[j])
         ifabs(corr) >0.5:  # 显著相似性的阈值
             G.add_edge(i, j, weight=corr)

我们将时间序列划分为20个片段。计算每对片段之间的皮尔逊相关系数,并将相关系数高于阈值的片段连接起来。

利用图连通性分析平稳性

相似图中的连通性可以揭示平稳性的洞见。如果片段高度连通(节点之间有许多边),这表明该序列在时间上具有平稳特性。如果只有很少或孤立的簇,则意味着该序列可能是非平稳的,在不同的片段中具有不同的时间模式。

基于图的平稳性度量

几个图度量可以量化这些属性:

聚类系数 :衡量节点形成紧密群组的倾向,这可能表明局部平稳性。

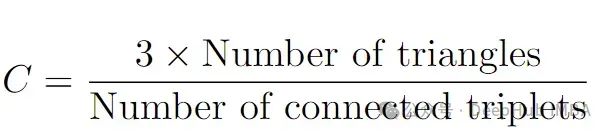
平均路径长度 :反映了时间序列片段的整体连通性和相似性。

模块度 :确定社区的存在,高模块度表明时间变化。

 clustering_coef=nx.average_clustering(G)
 avg_path_length=nx.average_shortest_path_length(G)
 
 print("Clustering Coefficient:", clustering_coef)
 print("Average Path Length:", avg_path_length)

通过图分区可视化平稳性

为了可视化时间结构,我们可以使用图分区来识别高度连通的节点簇,对应于相似或平稳的片段。例如,谱聚类可以突出显示平稳和非平稳簇。

为了演示我们创建了一个只有正边的新图,因为我们在示例中使用的社区检测算法需要正权重,而相关性也可以是负的。在这个例子中使用 R² 而不是相关性作为边权重重新创建了相同的图。

 fromnetworkx.algorithmsimportcommunity
 importcommunityascommunity_louvain
 
 # 应用 Louvain 社区检测
 partition=community_louvain.best_partition(G)

从社区图推断平稳性

一旦我们将时间序列转换为图,主要关注的就是片段在时间上的连通性。连通模式可以给我们关于时间序列平稳性的线索。具体如下:

高连通性(密集社区) :如果图显示节点(片段)之间的高连通性,很少或没有孤立的簇,这表明时间序列是平稳的。密集的社区或"充分混合"的结构意味着时间序列的统计特性(如均值和方差)随时间保持一致,这意味着整个过程中片段之间的相似性很高。

低连通性(稀疏社区) :如果图有几个稀疏或弱连通的簇,具有孤立的组或"分散"结构,这表明非平稳性。在非平稳时间序列中,某些片段可能具有不同的统计特性,例如变化的趋势、季节性变化或不同的方差。这些变化会破坏均匀连通性,导致只有某些片段彼此相似的簇。

模块度和社区结构 :图中高模块度(即片段形成不同的、分离良好的社区)表明数据中存在更强的非平稳趋势。例如,如果时间序列包含周期性循环或在不同制度之间转换(如金融数据中的不同市场状态),这些制度将形成可识别的簇。低模块度,其中节点是大型互连组件的一部分,通常反映了平稳性,因为片段随时间共享相似的统计特性。

聚类系数和最短路径 :高聚类系数(簇内有许多连接)和短平均路径长度(片段之间的"距离"低)通常伴随平稳时间序列。如果这些指标较低,某些节点之间的路径较长,则表明存在不同的时间制度或模式,表明非平稳性。

模拟不同平稳性和非平稳性程度的信号

为了更好地捕捉非平稳性,我们分析从三个离散状态扩展到连续的非平稳性尺度。这里将生成几个具有递增非平稳性水平的模拟信号,逐渐改变频率和幅度等统计特性。然后将计算并可视化每个信号的图度量,以观察它们如何在这个连续谱上变化。

按如下方式创建信号:

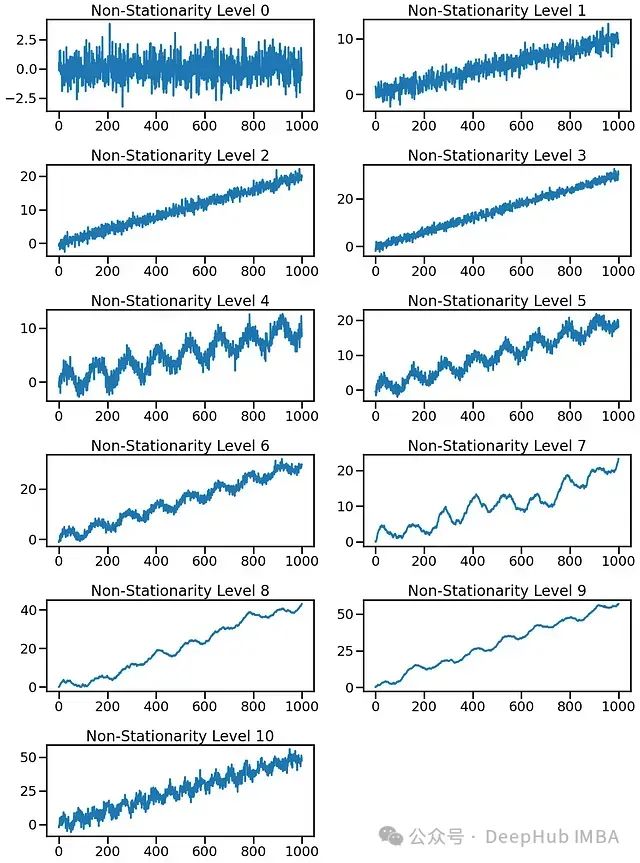
平稳(0级) :具有恒定均值和方差的纯白噪声。

低非平稳性(1-3级) :引入一个微妙的线性趋势来模拟轻微的漂移。

中等非平稳性(4-6级) :在趋势之上添加季节性成分,如周期性模式。

高非平稳性(7-9级) :引入随机游走成分,导致更多的可变性。

非常高的非平稳性(10级) :结合强趋势、高季节性和随机冲击,创建具有不同时间制度的信号。

每个级别通过逐步增加可变性和改变统计特性来增加非平稳性。

 N=1000
 time=np.arange(N)
 
 signals= []
 np.random.seed(42)
 
 forlevelinrange(11):
     iflevel==0:
         signal=np.random.normal(0, 1, N)
     eliflevel<=3:
         trend=0.01*level*time
         signal=np.random.normal(0, 1, N) +trend
     eliflevel<=6:
         trend=0.01* (level-3) *time
         seasonality=2*np.sin(0.05*time)
         signal=np.random.normal(0, 1, N) +trend+seasonality
     eliflevel<=9:
         trend=0.02* (level-6) *time
         seasonality=2*np.sin(0.05*time)
         random_walk=np.cumsum(np.random.normal(0, 0.2, N))
         signal=trend+seasonality+random_walk
     else:
         trend=0.05*time
         seasonality=3*np.sin(0.1*time)
         random_shocks=np.random.normal(0, 3, N)
         signal=trend+seasonality+random_shocks
     signals.append(signal)

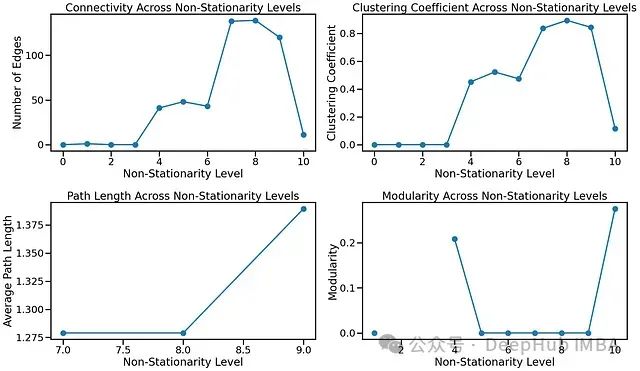
连通性(边数):

边数开始时较低,然后在非平稳性水平 5-8 左右迅速增加,表明存在一个过渡阶段,片段开始变得更加连通。

在最高的非平稳性水平(10级),连通性下降,这可能反映了由于强随机冲击和剧烈变化,片段在其特性上过于分散。

聚类系数:

在初始的非平稳性水平,聚类系数保持较低,这对于平稳或近乎平稳的信号是预期的,因为片段非常相似,只形成很少的强连接。

在 6-9 级左右显著增加,表明随着非平稳性的增加,片段开始聚集成小的、紧密连通的组。这可能反映了季节性或趋势性成分的影响,相似的片段形成簇。

在最高的非平稳性水平(10级),聚类系数急剧下降,这可能是由于片段变得不那么均匀连通,导致孤立的簇。

平均路径长度:

在较低的非平稳性水平,路径长度一致且相对较低,意味着一个连通良好的图,具有相似的片段。

在 8-9 级有明显的增加,表明随着非平稳性的增长,片段在连通性方面越来越远。

由于一些图是不连通的,路径长度测量似乎很稀疏,这可能表明片段已经失去了足够的相似性而无法保持连通。

模块度:

在 10 级,模块度显著增加,表明图更加分散,片段形成不同的社区。这是高度非平稳信号的特征,可能有几个不同的时间制度。

在中间的非平稳性水平,模块度相对较低,这表明片段足够相似,可以避免形成不同的社区,但由于小趋势或季节性,它们仍然表现出一些小的结构。

关键结果

从这个分析中,我们可以得出以下结论:

• 中等非平稳性下连通性和聚类的增加:5-8 级左右显示连通性和聚类的增加,反映了中等季节性或趋势成分的存在,其中片段变得更加相互关联。
• 非常高的非平稳性下的高模块度:10级显示了高模块度,这与显著的非平稳性一致。这是预期的,因为片段已经大大偏离,形成了不同的社区,使图变得支离破碎。
• 极端水平下聚类和连通性的下降:在非平稳性的极端,随着随机性占主导地位,连通性和聚类下降,导致稀疏连通或孤立的节点。

总结

本文探讨了利用图论分析时间序列数据平稳性与连通性的方法。通过将时间序列转换为图结构,计算片段间相似性,构建连通图,可以揭示数据的隐藏模式。文章介绍了平稳性的概念,提出了基于图的平稳性度量,展示了图分区在可视化平稳性中的应用。此外,本文还模拟了不同平稳性和非平稳性程度的信号,分析了图度量随非平稳性的变化。最后,总结了关键观察结果和启示,为时间序列数据分析提供了新的视角。

https://avoid.overfit.cn/post/475105042fa1446f8c7879b9faa3da56

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！