Python 3D建模指南【numpy-stl | pymesh | pytorch3d | solidpython | pyvista】

这篇文章介绍了Python 3D建模指南【numpy-stl | pymesh | pytorch3d | solidpython | pyvista】，分享给大家做个参考，收藏Python资料网收获更多编程知识

想象一下，我们需要用 python 编程语言构建某个对象的三维模型，然后将其可视化，或者准备一个文件以便在 3D 打印机上打印。 有几个库可以解决这些问题。 让我们看一下如何在 python 中从点、边和图元构建 3D 模型。 如何执行基本 3D 建模技术：移动、旋转、合并、减去等。

在线工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 3D场景编辑器

我们将使用以下Python库完成上述任务：

• numpy-stl
• pymesh
• pytorch3d
• SolidPython

使用每个库，我们构建门格尔海绵分形，将模型保存到 stl 文件，然后渲染图像。 在此过程中，我们简要了解了数据结构和术语。

所有示例均针对 Linux 操作系统提供，代码可以在 GitHub 存储库中找到。

1、环境准备

打开你的 Linux 终端并运行以下 shell 命令：

# Docker for Pymesh library examples:
curl -fsSL https://get.docker.com -o get-docker.sh
sudo sh get-docker.sh
# PyTorch3d g++ compiler:
sudo apt update
sudo apt install g++
# Repository cloning and library installation:
git clone https://github.com/format37/python3d.git
cd python3d
pip install -r requirements.txt
pip install "git+https://github.com/facebookresearch/pytorch3d.git"
# OpenScad install:
sudo apt-get install openscad

如果遇到安装问题，我建议你使用谷歌搜索。 不幸的是，随着时间的推移，一些依赖项可能会变得过时。 本文的主要思想是尽可能多地收集和概述 Python 3D 建模方法。

2、Numpy-stl概述

多边形网格的结构：

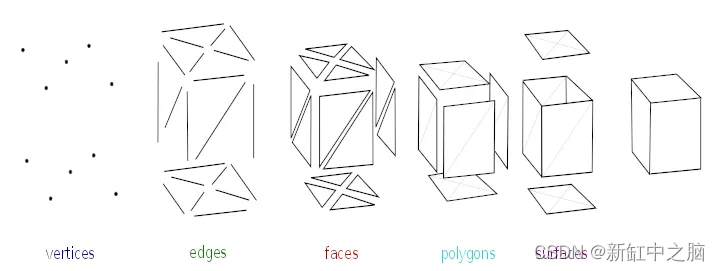
2.1 Vertices

点列表。 每个点由三个数字描述 - 3 维空间中的坐标。

接下来，我们将使用 Jupyter Notebook。

示例：numpy_stl_example_01.ipynb

import numpy as np
from myplot import plot_verticles
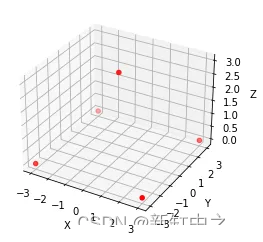
vertices = np.array([
[-3, -3, 0],
[+3, -3, 0],
[+3, +3, 0],
[-3, +3, 0],
[+0, +0, +3]
])
plot_verticles(vertices = vertices, isosurf = False)

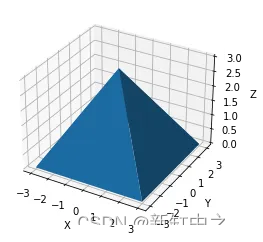
尽管仅描述了顶点，但已经可以想象如果将它们与三角形连接起来，模型会是什么样子：

plot_verticles(vertices = vertices, isosurf = True)

看起来这些面已经存在了。 但现在我们只有顶点。 要创建 STL 文件，我们需要描述面，这可以手动完成，或者使用scipy 库提供的 spatial.ConvexHull 函数完成操作。

示例：numpy_stl_example_02.ipynb

import numpy as np
from scipy import spatial
from stl import mesh
from myplot import plot_mesh
vertices = np.array(
[
[-3, -3, 0],
[+3, -3, 0],
[+3, +3, 0],
[-3, +3, 0],
[+0, +0, +3]
]
)
hull = spatial.ConvexHull(vertices)
faces = hull.simplices

faces 数组包含以下面描述：

array([
[4, 1, 0],
[4, 2, 1],
[3, 4, 0],
[3, 4, 2],
[3, 2, 1],
[3, 1, 0]
], dtype=int32)

2.2 Faces

面列表。 每个三角形面由三个顶点（点）描述。 换句话说，顶点数组中点的位置。

例如，最后一个面包含数字 3, 1, 0。因此面由顶点数组的第 0、1 和 3 个元素的点组装而成：

2.3 Mesh

网格是顶点和面的集合，确定多面体对象的形状。

myramid_mesh = mesh.Mesh(
  np.zeros(faces.shape[0], dtype=mesh.Mesh.dtype)
)
for i, f in enumerate(faces):
  for j in range(3):
    myramid_mesh.vectors[i][j] = vertices[f[j],:]
    plot_mesh(myramid_mesh)

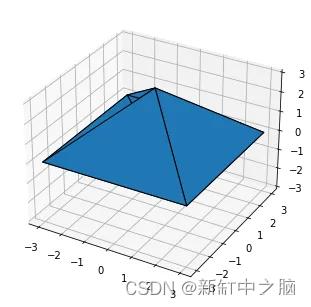
从图中可以看出，金字塔的一面是上下颠倒的。 在下面的例子中，在构造分形时，不会使用ConvexHull方法，因为它以任意顺序排列面的点，这会导致某些面的翻转。

myramid_mesh.save('numpy_stl_example_02.stl')

要查看 STL 文件，可以使用Blender，或者直接使用STL在线预览工具：

space.convexhull方法被设计用于计算凸壳，并且可以很好地应对金字塔和立方体。 但在有空腔的物体中，由于点的数量不一致，在组装STL时会丢失部分点，从而出现错误。

这在二维示例中清晰可见：numpy_stl_example_03.ipynb

import matplotlib.pyplot as plt
from scipy import spatial
import numpy as np
points = np.array([
[0,0],
[-2,0],
[-2,2],
[0,1.5],
[2,2],
[2,0]
])
hull = spatial.ConvexHull(points)

hull.simplices 包含面描述：

array([
[2, 1],
[2, 4],
[5, 1],
[5, 4]
], dtype=int32)

让我们绘制顶点和面：

plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
  plt.plot(points[simplex, 0], points[simplex, 1], 'k-')

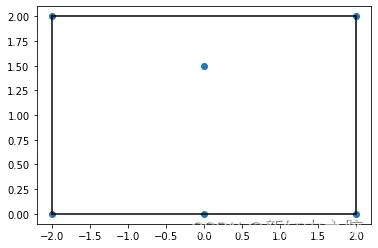
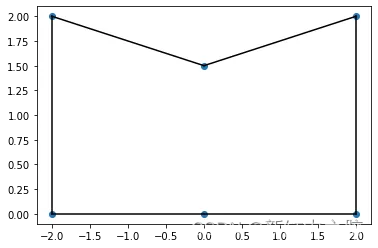
对于这种情况，可以找到凸包的替代方案，或者手动描述边：

faces = np.array([
[0, 1],
[1, 2],
[2, 3],
[3, 4],
[4, 5],
[5, 0]
])
plt.plot(points[:,0], points[:,1], 'o')
for simplex in faces:
  plt.plot(points[simplex, 0], points[simplex, 1], 'k-')

3、Numpy-stl构建分形

是时候构建一个分形了。 Numpy-stl 中没有布尔减法函数。 为了构建门格尔海绵分形，我们采取了相反的做法。 有两种方法：

• 构建基本立方体网格。 我们称之为体素。
• 将多个体素组合成一个网格。

我们将从立方体构建分形，就像从构造函数一样。

构造分形的逻辑描述：

假设分形面长度为1。分形深度是唯一孔尺寸的数量。 体素长度取决于分形的深度，每个新的深度级别都会除以 3。
我们将找到深度为 1 和 2 的体素边。让我们简化任务，将分形从 3 维变为 1 维情况：

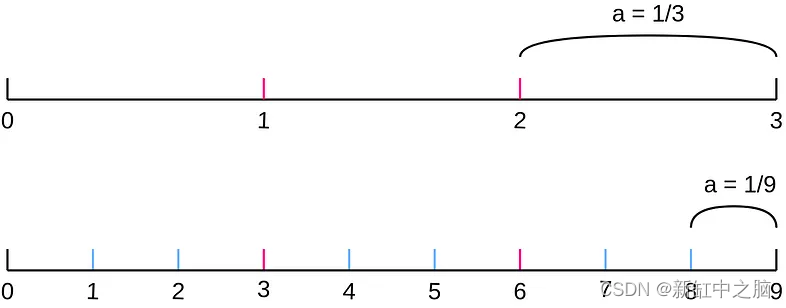
如果分形级别为 2，则立方体边长将为 1 / (3 ** 2)，相当于 1/9。 让我们制作一组立方体，以便它们按其位置填充生成的体素立方体。 我们来计算一下孔面积。 排除孔中的体素。 总之，将剩余的体素合并到一个对象中并保存。
示例：numpy_stl_example_04.ipynb

4、Numpy-stl渲染

为了渲染图像，我们将从 STL 文件加载的网格发送到plot_mesh 函数。

示例：numpy_stl_example_05.ipynb

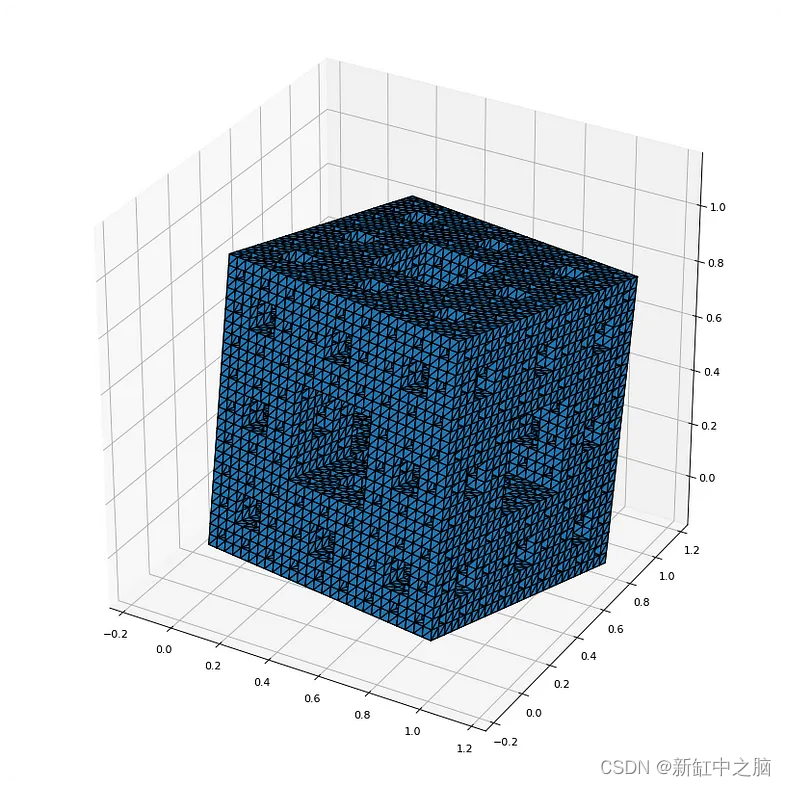
5、PyMesh概述

不幸的是，Pymesh 库无法通过 PIP 包管理器安装，尽管文档中描述了这种方法，也无法通过 Anaconda 安装。 有两种安装方法。

按照说明，从源代码进行编译。
使用docker容器。 我选择这个选项是因为更有趣。 容器使用参数启动。 使用启动参数，将脚本文件夹装载到容器中。 让我们为脚本提供必要的参数。 脚本执行完成后，容器将被删除。
如果Docker已经按照文章开头的说明安装，则无需再安装。如果 Docker 不适合你，请按照文档中的说明编译 Pymesh。 这个选项也经过我的测试。

示例：pymesh_example_01.py

import pymesh
box_a = pymesh.generate_box_mesh([0,0,0], [1,1,1])
filename = "/pymesh_examples/pymesh_example_01.stl"
pymesh.save_mesh(filename, box_a, ascii=False)

从项目根目录启动容器：

sh pymesh_example_01.sh

执行上述命令后：

• Pymesh 容器启动。 初次启动镜像下载需要一些时间。
• Pymesh_examples 文件夹安装在容器内。
• Python 脚本在容器内启动： /pymesh_examples/pymesh_example_01.py
• Pymesh 库已导入。
• generate_box_mesh 函数根据点 [0,0,0] 和 [1,1,1] 处的两个相对顶点生成立方体。
• Save_Mesh 函数将对象保存在 STL 文件中。

执行后， pymesh_examples文件夹中出现 pymesh_example_01.stl文件。

让我们使用布尔减法来制作一个方孔。 我们要构建一个平行六面体并将其从主立方体中减去。

示例：pymesh_example_02.py

import pymesh
box_a = pymesh.generate_box_mesh([0,0,0], [1,1,1])
box_b = pymesh.generate_box_mesh([0.4,0.4,0], [0.6,0.6,1])
box_c = pymesh.boolean(
  box_a,
  box_b,
  operation='difference',
  engine="igl"
)
filename = "/pymesh_examples/pymesh_example_02.stl"
pymesh.save_mesh(filename, box_c, ascii=False)

运行程序：

sh pymesh_example_02.sh

布尔函数很简单。 第一个参数是我们从中减去的对象。 其次是我们做减法。 我们还发送操作和引擎。

布尔值不仅适用于减法。 总共有 4 种操作可用：

• 交：A∩B
• 并：A∪B
• 差：A∖B（最后两个例子）
• 异或：A XOR B（图像未显示）

为了更好地理解如何移动和旋转对象，出于调试目的，可以方便地暂时用 Union 代替 Difference 操作。

让我们制作第二个孔，移动并旋转它。

示例：pymesh_example_03.py

运行：

sh pymesh_example_03.sh

我们的脚本包含了移动和旋转函数。 通过移动，会根据原始对象修改后的顶点和面创建一个新的网格对象。四元数类描述旋转，然后根据原始对象的顶点和面以及旋转的描述创建一个新的旋转对象。

脚本执行的结果是一个带有两个相交孔的立方体：

这些工具足以构建分形。

6、PyMesh构建分形

示例：pymesh_example_04.py

在此脚本中，我们添加了一个输入参数来设置分形深度。 对于每个深度级别，创建一个框，复制两次，然后旋转和偏移。 结果只有 3 个平行六面体，这是从主立方体中减去的。 每条边各一个。 此操作重复 x 和 y 次以填充所有行和列边缘。 未执行从空白空间中减去的检查。

这次我们必须明确指定分形的深度：

sh pymesh_example_04.sh 3

需要 5 至 15 分钟才能完成。 启动后，新的STL文件将出现在 pymesh_examples文件夹中：

请求 4 级分形，组装大约需要 4 小时，文件大小为 73 mb：

3D打印后就是这样：

7、PyMesh渲染

上次我们旋转了网格。 这次让我们旋转相机。

示例：pymesh_example_05.py

运行程序：

sh pymesh_example_05.sh

8、PyTorch3d概述

金字塔示例：pytorch3d_example_01.py

方法与 numpy-stl 中使用的方法非常相似。 但由于它应该在 GPU 上工作，因此我们将主机和设备的概念分开。

• 主机就是我们的电脑。
• 设备是显卡。如果你没有显卡，仍然可以使用库，那么CPU将充当GPU。

主机和设备都有自己的内存。 要将项目从主机传输到设备并传回，我们需要执行一个小仪式。

在下面的例子中，我们立即描述设备上的顶点，将它们从设备复制到主机。 基于顶点计算的边。 然后保存该对象。 生成的 OBJ 文件可以导入到Blender中：

注意命令 verts.cpu().numpy()

顶点从设备复制到主机。 如果使用 GPU，每个副本都会减慢算法速度。 在规划程序架构时，最好将主机和设备之间的复制操作次数尽可能减少。 例如，如果你最初在主机上有一个顶点列表，则可以计算面，而无需将顶点从设备复制到主机，如下一个示例中所示。

示例：pytorch3d_example_02.py

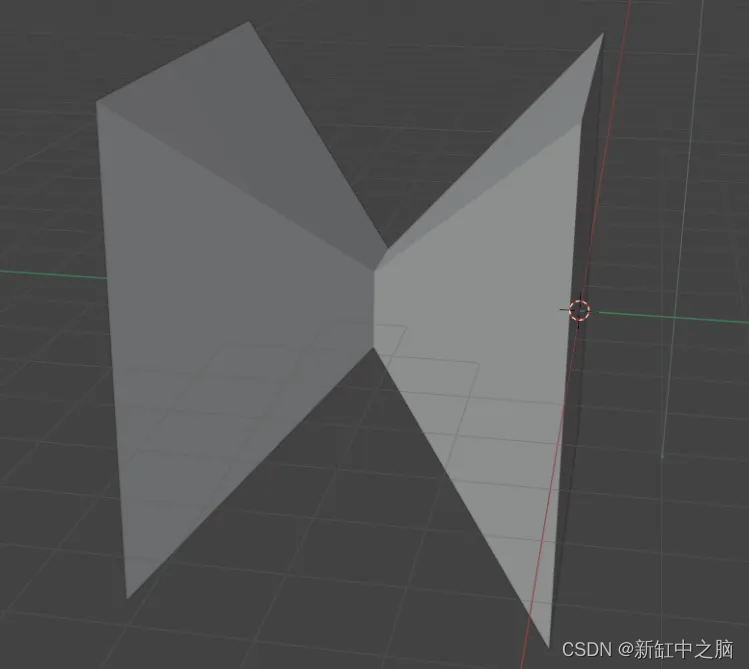
9、PyTorch3d构建分形

GPU 提供了一些性能提升。

示例：pytorch3d_example_03.py

我们声明了指定深度级别的最小体素的顶点。 使用与前面的示例相似的算法，我们计算二维的孔坐标。 然后用不会落入孔中的体素填充主立方体。

计算速度提高了一个数量级，这使得在大约 5 小时内构建 5 级分形成为可能：

此 STL 文件的大小为 1.9 GB。 在构建第 5 层分形时，由于显卡内存溢出，程序停止。 我必须分批收集该物体。 创建了 10 层“2D”分形，然后将它们附加到主要对象上，直到构建完整的分形。

10、PyTorch3d渲染

除了绘图可视化之外，pytorch3d 还特别关注渲染。 而且这种方法非常彻底，有纹理和着色器。

示例：pytorch3d_example_04.py

11、SolidPython概述

SolidPython 是目前最丰富的建模库。 3D场景，描述格式，与openscad非常相似。 Python 生成写入 scad 文件的 openscad 代码。 然后可以在openscad中编辑或立即保存为STL。

示例：solidpython_example_01.ipynb

from solid import *
d = difference()(
  cube(size = 10, center = True),
  sphere(r = 6.5, segments=300)
)
path = scad_render_to_file(d, 'solidpython_example_01.scad')

为了指定球体的分辨率，我们使用 word segment，而不是通常的 $fn openscad 参数。

Solidpython 方便调试。

• 在屏幕的一侧，我们打开了 scad 文件。
• 在另一边，我们打开了 Jupyter Notebook。

在 Jupyter Notebook 中执行 scad_render_to_file 后，openscad 中的图片会自动更新。

Openscad 可以使用控制台命令将模型渲染为 stl 文件。 Jupyter 笔记本中有调用示例：

!openscad solidpython_example_01.scad -o solidpython_example_01.stl

任何 openscad 函数都会返回一个对象。

要对对象执行操作，请在操作调用字符串末尾的圆括号中传递对象或对象列表。

示例：solidpython_example_02.ipynb

from solid import *
c = circle(r = 1)
t = translate([2, 0, 0]) (c)
e = linear_extrude(
  height = 10,
  center = True,
  convexity = 10,
  twist = -500,
  slices = 500
) (t)
col = color('lightgreen') (e)
path = scad_render_to_file(col, 'solidpython_example_02.scad')

分辨率由切片参数决定。

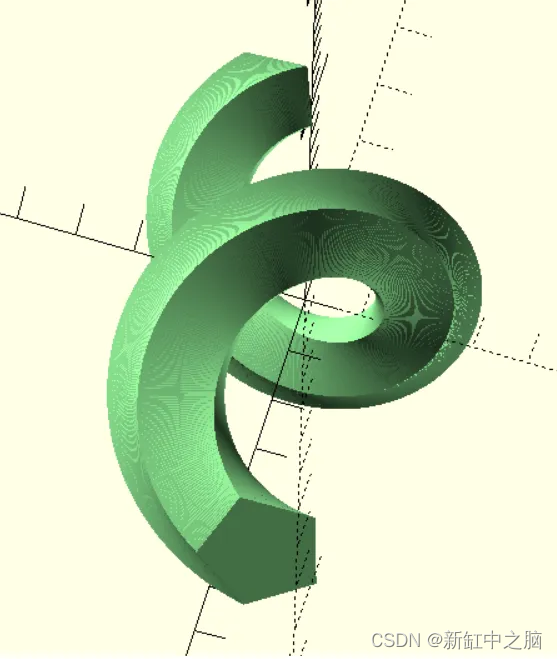
12、SolidPython构建分形

示例：solidpython_example_03.ipynb

13、SolidPython渲染

让我们通过相机在每个图像上旋转来渲染最后一个场景的一系列图像。

示例：solidpython_example_04.ipynb

此外，solidpython 还提供使用 openscad 的动画生成功能。 文档中有一小节带有示例。

最后，让我们看一下本文标题中用于构建场景的代码。

示例：solidpython_example_05.ipynb

14、PyVista

我还想提一下另一个有趣的 PyVista 库。

通过可视化工具包 (VTK) 的简化界面进行 3D 绘图和网格分析

他通过从 STL 文件读取网格来帮助我可视化深度图。 但除此之外，它还有一些其他有趣的功能。

15、库比较

目前的性能比较并不完全客观，因为算法存在显着差异。 Pymesh 和 SolidPython 使用减法，而 Numpy-stl 和 Pytorch3d 使用网格并集。

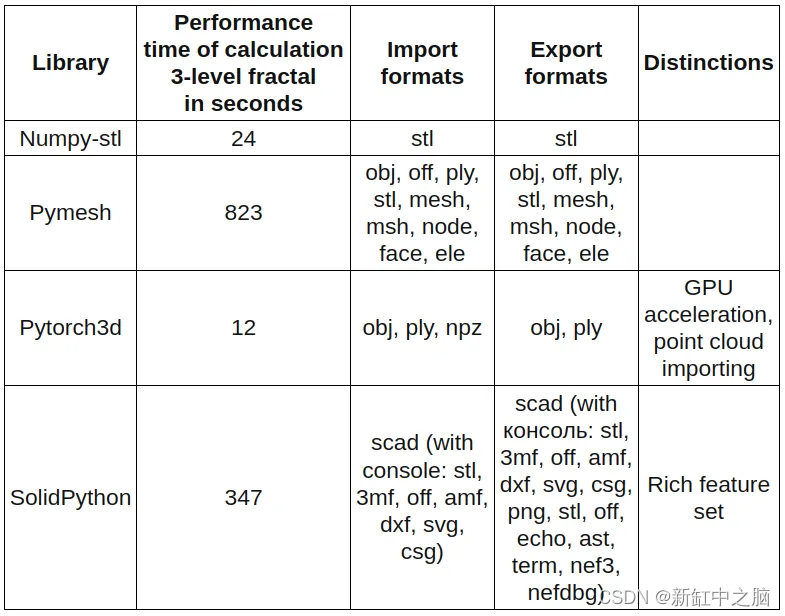
我的机器配置如下：

• Ubuntu 20.04.2 LTS
• Python 3.7.3
• 英特尔® 酷睿™ i3-7350K CPU @ 4.20GHz
• 内存 35.2Gb
• GPU GeForce GTX 1080 Ti 11175 MB

---

原文链接：Python 3D建模入门 — BimAnt

版权声明：本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！